Prolog: Der Raum als Paradoxon
Der Alltagsverstand sagt uns, dass wir vom Raum umgeben sind, wir sind augenscheinlich im Raum. Doch niemals nehmen wir den Raum selbst wahr. Woher wissen wir, dass es ihn gibt? Und wenn sich alles im Raum befindet, wo ist dann der Raum selbst? Was bleibt übrig, wenn wir uns alle Dinge einfach wegdenken?
1. Zenons Raum-Paradox
Aristoteles macht auf Zenon aufmerksam, der verdeutlichte, dass der Raum offenbar weder etwas „Stoffliches“ noch eine „Form“ sein kann:
„Die Schwierigkeit, die nun aber Zenon aufwarf: Wenn ‚Ort‘ etwas Seiendes ist, so muß er doch ‚in etwas‘ sein, – das aufzulösen ist nicht schwer: Es besteht ja gar kein Hinderungsgrund, daß der unmittelbare Ort ‚in einem Anderen‘ sei, allerdings an ihm nicht als an einem Ort, sondern so, wie ‚Gesundheit‘ (besteht) in den warmen (Anteilen des Körpers), als Verhältnis, die Wärme aber im Körper ist, als Zustand. Man muß also gar nicht notwendig ins Unendliche damit fortgehen. […], so kann ‚Ort‘ weder der Stoff noch die Form sein, sondern nur ein davon Verschiedenes.“ (Aristoteles, 4. Buch, Kap. 3, S. 94)
2. Kants erste Antinomie (Kosmologisches Raum-Zeit-Problem)
Im Teil „Die Transzendentale Dialektik“ seiner „Kritik der reinen Vernunft“ zeigt Kant u. a., dass die beiden folgenden, einander widersprechenden Sätze gleichermaßen bewiesen werden können: „Die Welt ist endlich.“ (Thesis) und „Die Welt ist unendlich.“ (Antithesis). Er löst die Antinomie mit dem Hinweis auf, dass uns die Welt niemals als Totalität, als etwas An-sich-Seiendes gegeben ist, sondern stets nur als unfertige Erscheinung: Weder können wir eine endgültige (für immer feststehende) Grenze erkennen, noch erreichen wir ein Ende der Erkenntnis, und somit kann die Welt für uns weder endlich (im Sinne einer für immer feststehenden Grenze) noch unendlich sein. Sowohl die Thesis als auch die Antithesis seien somit als falsch zurückzuweisen. (vgl. Gölz, 2008, S. 128 f.)
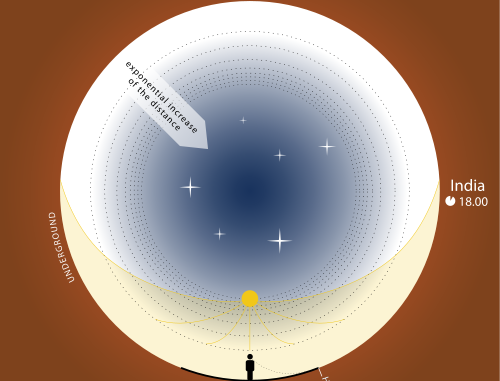
3. Olberssches Paradoxon
Dieses Paradoxon wurde erstmals von Heinrich Wilhelm Olbers formuliert. Betroffen sind Weltmodelle, die von einem unendlich ausgedehnten Universum mit gleichmäßiger Sternverteilung über große Distanzen ausgehen. Demnach hätte nach hinreichend langer Zeit das Licht jedes Sterns aus jeder Richtung die Erde erreicht, und damit müsste der Himmel mindestens so hell wie die Sternenoberfläche erscheinen. Der dunkle Nachthimmel spricht dagegen, was ein historisches Argument gegen solche Weltmodelle war.
Die heutige Erklärung basiert auf der allgemeinen Relativitätstheorie. Das Universum könnte durchaus unendlich ausgedehnt sein. Wegen seines endlichen Alters und der Endlichkeit der Lichtgeschwindigkeit erreicht uns seit dem Urknall nur Licht aus einem endlich großen Bereich. Hinzu kommen noch weitere Effekte, die mit der Expansion des Universums im Zusammenhang stehen. Durch die Ausdehnung des Universums verringert sich die Energie des uns erreichenden Lichtes. Dieses wird dadurch langwelliger (rötlicher). Es wird von einer kosmologischen Rotverschiebung gesprochen (vgl. Olbers’sches Paradoxon, physik.cosmos-indirekt.de).
4. Blockuniversum
Im Blockuniversum werden (im Gegensatz zur herkömmlichen Sicht der Raum-Zeit, bei der nur gegenwärtige Ereignisse als wirklich betrachtet werden) alle Geschehnisse und Objekte in der Raum-Zeit als „gleichwirklich“ in einem „vierdimensionalen Block“ ausgebreitet gedacht. Dies scheint zunächst insofern kontraintuitiv, als häufig unter „real“ das verstanden wird, was in der „Gegenwart“ kausal wirksam wird.
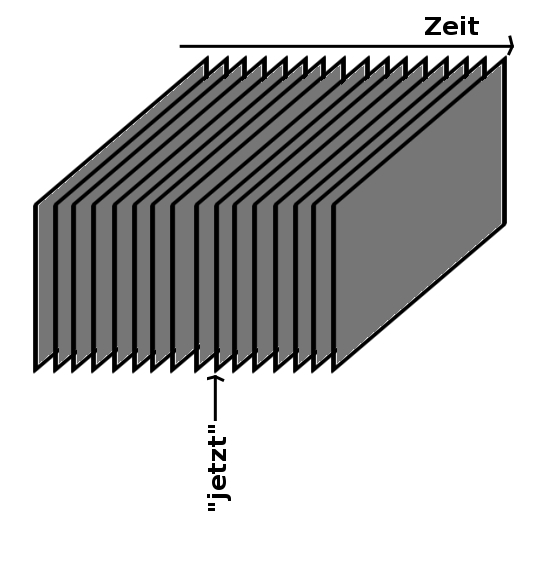
(Abbildung Blockuniversum: herkömmliche Sicht der Raum-Zeit versus Blockuniversum, Quelle: M. Bäker [19.09.2012])
Im Blockuniversum sind Zukunft und Vergangenheit „gleich wirklich“, und alle Objekte existieren in Gegenwart, Vergangenheit und Zukunft „gleich real“. Damit wäre die Vergangenheit sozusagen für „ewig konserviert“ und die Zukunft schon fest vorherbestimmt. Diese Position wird auch als Eternalismus bezeichnet. Freiheit hat in ein einem solchem Universum keinen Platz mehr.
Im Hinblick auf ihre empirischen Konsequenzen unterscheiden sich Blockuniversum und herkömmliches Universum offenbar nicht voneinander. Damit scheint auch die Wahl zwischen beiden Kosmos-Varianten nur vom zugrundeliegenden Realitätskriterium abzuhängen. Wofür wir uns entscheiden, ist eine Frage des „philosophischen Geschmacks“, die empirisch nicht entscheidbar ist.
5. Die Freiheit der Koordinatenwahl und die Hohlweltparadoxie
Wollen wir den Raum vermessen, benötigen wir Maßstäbe (z. B. Lineale, Vergleichskörper, Lichtstrahlen). Allerdings lässt sich eine solche Vermessung nicht vornehmen ohne entsprechende Hintergrundannahmen: z. B. Starrheit der Maßstäbe, Geradlinigkeit der Lichtstrahlen, Konstanz der Lichtgeschwindigkeit. Dabei gibt es grundsätzlich zwei Möglichkeiten: Entweder legen wir uns auf eine bestimmte Geometrie fest und bestimmen, wie sich die Maßstäbe zu verhalten haben (z. B. müssten sie sich in einer bestimmten Art und Weise verformen, damit wir an einer euklidischen Geometrie festhalten können) oder wir nehmen die Maßstäbe als starr an und ermitteln die daraus resultierende Geometrie (etwa eine nicht-euklidische). Die Frage der Raumgeometrie ist somit eine Frage der Konvention.
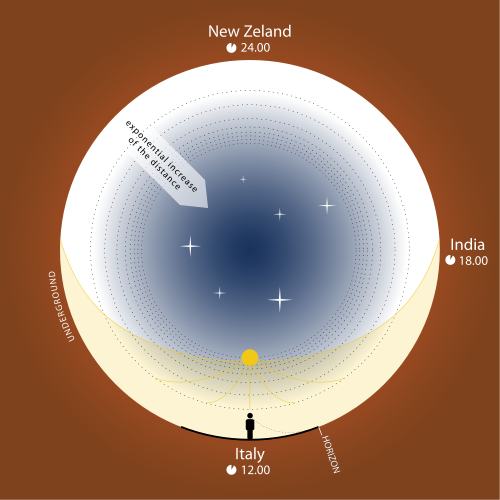
(Quelle: Von Joshua Cesa – eigenes Werk, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=10485406)
Ein besonders drastisches Beispiel dieser sogenannten Konventionalitätsthese ist die Hohlwelttheorie, die bereits Ende des 19. Jahrhunderts aufgestellt und 1933 in dem Buch „Das neue Weltbild“ von Johannes Lang weiterentwickelt wurde. (Carrier, Raum-Zeit, S. 131 ff.) Die Hohlwelttheorie geht von der Vorstellung aus, dass die Welt eine Hohlkugel ist, in deren Inneren wir leben. Damit würden alle Maßstäbe gleichermaßen in Richtung Kugelmittelpunkt schrumpfen und die Lichtgeschwindigkeit wird raumabhängig. Die Sonne hätte von der Erdoberfläche Richtung Kugelmittelpunkt einen Abstand von 300 m, noch dichter am Kugelmittelpunkt konzentrieren sich die extragalaktischen Objekte. Weder ein Durchbohrversuch durch die Erdoberfläche noch der Hinweis auf die Singularität des P Kugelmittelpunktes können die Hohlwelttheorie aushebeln. Immer wieder lässt sich diese Theorie durch geschickte Zusatzannahmen mit der Erfahrung in Einklang bringen. Empirisch ist die Hohlwelttheorie nicht widerlegbar.
6. Das Loch-Paradoxon und die Subtanzialismus-Relationalismus-Kontroverse
Die sogenannte Leibniz-Clarke-(Newton-)Kontroverse wurde im (auf die Jahre 1715/16 zu datierenden) Briefwechsel zwischen Leibniz und Newtons Vertrautem Clarke ausgefochten. Leibniz betrachtete den Raum als Gesamtheit relativer Lagebeziehungen und Anordnungen der Körper (Relationalismus). Dem steht Newtons Konzeption eines absoluten Raumes und einer absoluten Zeit, die beide ohne Beziehung auf einen äußeren Gegenstand bestehen (Substanzialismus), entgegen. Newton, der mit Gedankenexperimenten (Eimerversuch und Doppelkugelexperiment) überzeugende Belege (die teilweise bis heute noch gültig sind) angeben konnte, schien als Überlegener aus dieser Kontroverse hervorgegangen zu sein.
Der Newton’sche Eimerversuch
Ein mit Wasser gefüllter Eimer, der anfänglich ruht (Fall I), beginnt schnell zu rotieren. Im ersten Moment kann das Wasser der Bewegung noch nicht folgen, weshalb die Oberfläche flach bleibt (Fall II). Schließlich rotieren Eimer und Wasser gemeinsam, die Wasseroberfläche ist gekrümmt (Fall III). Plötzlich bleibt der Eimer stehen, aber das Wasser rotiert noch nach, weshalb die Oberfläche noch gekrümmt ist (Fall IV).
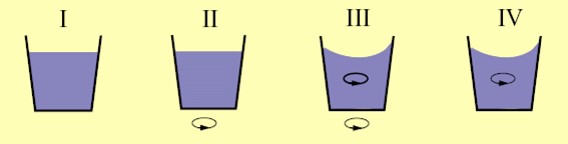
Wodurch wird die Krümmung der Wasseroberfläche verursacht? Es kann nicht die Relativbewegung zwischen Wasser und Eimer sein, wie die Vertreter des Relationalismus behaupten würden. Dagegen sprechen die Fälle II und III. In den Fällen III und IV findet aber eine Relativbewegung gegenüber dem absoluten Raum statt. Also muss der absolute Raum die Ursache der Krümmung der Wasseroberfläche sein. Da vom absoluten Raum reale Wirkungen ausgehen, muss er existieren.
Eine Neuauflage erfuhr diese Debatte ab dem Ende der 1980er-Jahre mit dem sogenannten Loch-Argument (vgl. z. B.: Norton, „Einstein, the Hole Argument and the Reality of Space“, S. 153–188; Earman, World Enough and Space-Time), das einen Relationalismus stützte.
Das Loch-Argument
In einem materiefreien Raumbereich („Loch“) lässt sich die Raum-Zeit-Struktur (dargestellt durch das sogenannte metrische Feld g) durch die Verteilung der Materie außerhalb nicht eindeutig festlegen. Innerhalb des „Loches“ sind gleichberechtigt verschiedene Zustände möglich. Im Bild links passiert die Galaxie den Raum-Zeit-Punkt (bzw. das Ereignis) E. Nach einer Koordinatentransformation (eine rein mathematische Prozedur, kein physikalischer Prozess!) passiert die Galaxie den Raum-Zeit-Punkt (bzw. das Ereignis) E nicht mehr (Bild rechts). Da wir aber physikalisch nicht unterscheiden können, ob die Galaxie den Raum-Zeit-Punkt (bzw. das Ereignis) E passiert oder nicht, kann der Raum (bzw. die Raum-Zeit) nicht als etwas Substanzielles (Absolutes) betrachtet werden. Es wird ein Relationalismus des Raumes gestützt.
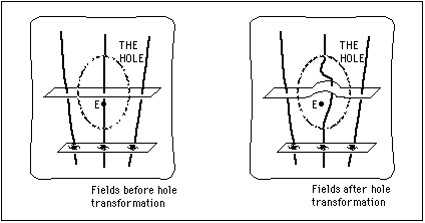
Der relationalistischen Interpretation der Raum-Zeit steht entgegen, dass die allgemeine Relativitätstheorie eben auch absolute Züge der Raum-Zeit aufdeckt. Dies zeigt sich daran, dass das metrische Feld g direkt auf das Material (im Sinne eines physikalischen Feldes, wie etwa magnetisches oder elektrisches Feld) zurückwirkt. Die Raum-Zeit verhält sich damit wie physikalische Materie. Dies zeigt sich z. B. am Nachweis von Gravitationswellen (Raum-Zeit-Deformationen, die reale Wirkungen zeigen) oder an der Existenz von Lösungen der Einstein’schen Gravitationsfeldgleichungen, bei denen ein komplett materiefreier Raum über eine Krümmung verfügt (z. B. der Anti-De-Sitter-Kosmos).
Der Anti-De-Sitter-Kosmos
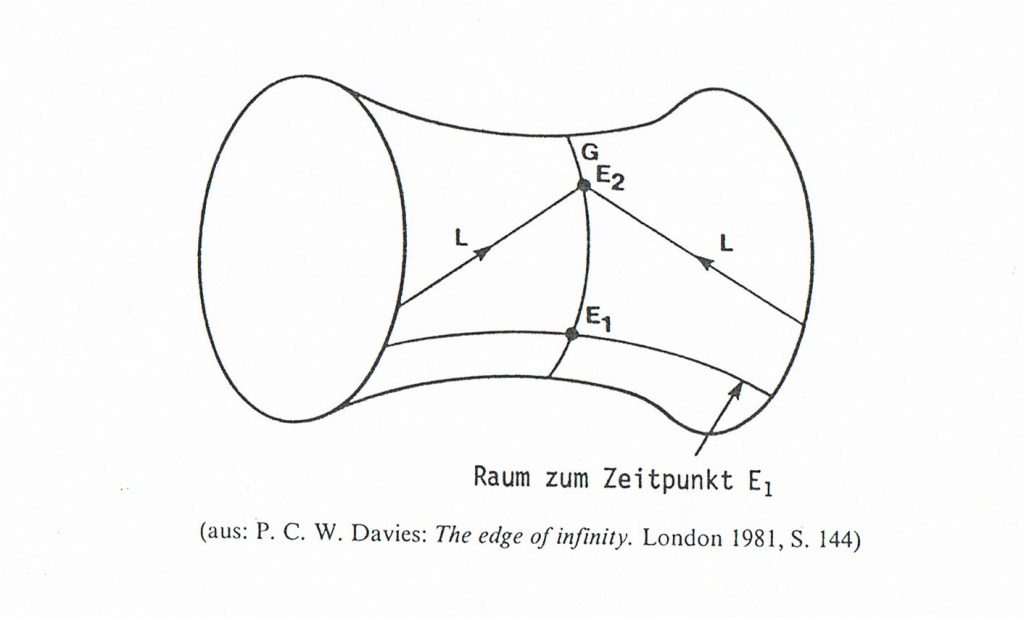
Der Anti-De-Sitter-Kosmos ist nach dem niederländischen Astronomen Willem de Sitter benannt. Es handelt sich hierbei um eine Lösung der Einstein’schen Gravitationsfeldgleichungen. Der Anti-De-Sitter-Kosmos ist ein statischer Kosmos, d. h., er kann weder expandieren noch kontrahieren. Interessanterweise verläuft die Zeit auf einer geschlossenen Kurve. D. h., jedes Ereignis kehrt nach einer bestimmten Zeit wieder, etwa im Sinne des Filmklassikers „Und täglich grüßt das Murmeltier“ (1993). Der Anti-De-Sitter-Kosmos wäre die perfekte Realisierung einer Zeitmaschine.
Die Raum-Zeit erscheint damit als ein paradoxes „Zwitterwesen“: Einerseits ist sie als physikalisches Feld der Materie selbst zuzurechnen, andererseits erscheint Raum als ein Relationsbegriff ohne materielle Grundlage.
7. „Gehirne im Tank“, „Matrix“ und Außenweltskeptizismus
Der Außenweltskeptizismus taucht in unterschiedlichen Varianten auf. Eine frühe Version ist ein Gedankenexperiment von René Descartes: Könnten wir nicht zumindest als Hypothese annehmen, dass uns ein böser Dämon täuscht, indem er uns eine Welt vorgaukelt, die so gar nicht besteht. Ein berühmtes Revival des Außenweltskeptizismus ist Putnams Gedankenexperiment der „Gehirne im Tank“, das in dem Film „Matrix“ eine künstlerische Umsetzung erfahren hat. Man kann diesen Gedanken weiterspinnen: Was ist, wenn das Universum bloß aus automatischen Apparaten besteht, die einen Tank voller Gehirne und Nervensysteme kontrollieren und allen eine kollektive Halluzination vorspiegeln? Dieser Gedanke ist absurd, aber lässt er sich auch nicht widerlegen.

(Chalmers, The Character of Consciousness, S. 456)
Man kann diesen Gedanken insofern weiterführen, als man skeptisch sein sollte, ob der Begriff der „Außenwelt“ überhaupt ein sinnvoller Begriff ist. Der Grund ist, dass wir uns stets eben nur in unserem kognitiven Raum befinden, aus dem wir auch nicht heraustreten können, um zu schauen, ob etwas „außerhalb“ ist.
Die Neurowissenschaften scheinen zudem zu bestätigen, dass die räumlich-zeitliche Dingwelt (von uns als „Außenwelt“ erfahren) vom Gehirn erst konstituiert wird. Erst das Gehirn erzeugt ein „Drinnen“ und „Draußen“. Das Räumlich-Dingliche besteht also nur im Rahmen unserer kognitiven Welt. Die Rede von einer räumlich-dinglichen Außenwelt hat insofern wenig Sinn, als dies eine Art „Hyperraum“ suggeriert, der beide Welten umfasst. Auch das dem Neurologen zugängliche menschliche Gehirn existiert nur innerhalb seines kognitiven Raumes (vgl. Roth, 1987 S. 238 ff.).
Epilog: Ist der Außenweltbegriff überhaupt sinnvoll?
Vielleicht hat ein Gutteil der Raum-Paradoxien seine Ursache in einer Hypostasierung (im Sinne einer Vergegenständlichung, Verdinglichung einer Eigenschaft, eines Begriffs, eines bloßen Gedankens) des Konzeptes Raum zu einer (physischen) Außenwelt. Möglicherweise ist der Schlüssel zum Verständnis dessen, was der Raum ist, in den Ansätzen subjektivistischer Philosophen, wie etwa Berkeley, Hume, Kant, Fichte, Schelling, Schopenhauer, Husserl, Mach, aber auch im Radikalen Konstruktivismus, zu suchen. Schopenhauer bringt diese Sicht gleich zu Beginn seines Werkes „Die Welt als Wille und Vorstellung“ auf die knappe Formel:
„‚Die Welt ist meine Vorstellung‘ – dies ist eine Wahrheit, welche in Beziehung auf jedes lebende und erkennende Wesen gilt; […]; daß die Welt, welche ihn [KH: den Menschen] umgibt, nur als Vorstellung da ist, d. h. durchweg nur in Beziehung auf ein anderes, das Vorstellende, welches er selbst ist.“ (Schopenhauer, Die Welt als Wille und Vorstellung I, § 1, S. 31)
In diesem Sinne könnte man sagen: Wenn es den Raum gibt, so gibt es ihn nur im Subjekt, als ein Strukturkonzept, das die Vorstellung von einer Außenwelt erst möglich macht. Dies schließt auch die Dualität des physikalischen Raumes (bzw. der Raum-Zeit) nicht aus, einerseits als eine Art physikalisches Objekt (in Analogie zu physikalischen Feldern, wie elektrisches oder magnetisches Feld) in Erscheinung zu treten, das mit anderen physikalischen Objekten kausal verbunden ist (Substanzcharakter oder absoluter Charakter), und andererseits nur ein relationales Ordnungsprinzip sein. Denn nach subjektivistischer Sicht sind eben auch die physikalischen Objekte (sowie die Kausalbeziehungen zwischen ihnen) Ordnungsprinzipien bzw. begriffliche Konzepte oder Konstruktionen; was sie aber darüber hinaus sind, lässt sich nicht sinnvoll beantworten.
Literatur
Aristoteles: Philosophische Schriften in sechs Bänden (übersetzt von Hans Günther Zekl). Physik. Vorlesung über Natur, Band 6. Hamburg 2019.
Carrier, Martin: Raum-Zeit. Berlin 2009.
Chalmers, David: The Character of Consciousness. Oxford 2010.
Earman, J.: World Enough and Space-Time, Cambridge Mass. 1989.
Gölz, Walter: Kants „Kritik der reinen Vernunft im Klartext“. 2. Auflage. Tübingen 2008.
Norton, J.: „Einstein, the Hole Argument and the Reality of Space“. In: J. Forge (Hrsg.), Measurement, Realism and Objectivity, Dordrecht 1987, S. 153–188.
Roth, Gerhard: Erkenntnis und Realität: Das Gehirn und seine Wirklichkeit. In: Der Diskurs des Radikalen Konstruktivismus. Hrsg. von Siegfried J. Schmidt. Frankfurt a. M. 1987, S. 229 – 255.
Schopenhauer, Arthur: Die Welt als Wille und Vorstellung I. In: Sämtliche Werke. Hrsg. von Wolfgang Frhr. Von Löhneysen. Band 1. Hamburg 2018.
Internetquellen
Olberssches Paradoxon https://physik.cosmos-indirekt.de/Physik-Schule/Olberssches_Paradoxon (Aufruf: 19.08.2020)
Prof. Dr. phil. Dipl.-Phys. Kay Herrmann
Technische Universität Chemnitz
Philosophische Fakultät
Institut für Pädagogik (IfPäd)
Reichenhainer Str. 41/018
09126 Chemnitz
(mail) kay.herrmann@phil.tu-chemnitz.de






